Main research interests & current projects
EOR using foam (SAG)
Mathematical and computational modeling of foam injection as an enhanced oil recovery technique applied to Brazil pre-salt reservoirs.
It is an international collaboration between UFJF (Federal University of Juiz de Fora, Brazil), TU Delft (Delft University of Technology, Holland) and PUC-Rio (Pontifical Catholic University of Rio de Janeiro, Brazil) supported by Shell Brazil
The main objectives of this 4-year project are:
- Improve the understanding of physics and mathematics describing the foam displacement in porous media as an enhanced oil recovery (EOR) technique applied to Brazil pre-salt reservoirs.
- Develop analytic and numerical methods that can be used to test and validate commercial simulators.
The project has a strongly multidisciplinary appeal bringing together the mathematical analysis and numerical simulations performed in UFJF, experimental investigation realized in PUC-Rio and physical modeling assisted by renowned experts in foam EOR from TU Delft.
Related papers
Valdez, A. R., Rocha, B. M., Chapiro, G., Weber, R. S., Uncertainty quantification and sensitivity analysis for relative permeability models of two-phase flow in porous media. Journal of Petroleum Science and Engineering, v. 192, p. 107297, 2020.
de Paula, F. F., Quinelato, T. O., Igreja, I. H. A., Chapiro, G., A Numerical Algorithm to Solve the Two-Phase Flow in Porous Media Including Foam Displacement., Lecture Notes in Computer Science, v. 12143, p. 18-31, 2020.
Thermal EOR
Combustion traveling waves
Filtration combustion is a thermal technique with great potential for use in the exploration of offshore oil, as in the case of the pre-salt reservoirs. The modeling of combustion in porous media involves Fluid Dynamics and Chemical Kinetics. The models describing in-situ combustion are composed of reaction-convection-diffusion equations, present different scales (stiff problems), and are difficult to solve both mathematically and computationally.
This project is focused on Applied Mathematics and proposes to develop research in the intersection between areas of Partial Differential Equations and Dynamical Systems aiming at applications in Petroleum Engineering.
Related papers
Zavala, R. Q., Chapiro, G.., Classification of the traveling wave solutions for filtration combustion considering thermal losses. Combustion and Flame, v. 219, p. 416-424, 2020.
Ozbag, F., Schecter, S., Chapiro, G., Traveling waves in a simplified gas-solid combustion model in porous media. Advances in Differential Equations, Volume 23, Number 5/6, 409-454, 2018.
Pereira, W., S., Chapiro, G., Numerical Validation of Analytical Estimates for Propagation of Thermal Waves Generated by Gas-Solid Combustion, Geofluids, Volume 2017, Article ID 1806052, 2017.
Chapiro, G., Senos, L., Riemann solutions for counter flow combustion in
light porous foam. Computational and Applied Mathematics, 2017.
Chapiro, G., Marchesin, D., The effect of thermal losses on traveling waves for in-situ combustion in porous medium. Journal of Physics. Conference Series (Print), v. 633, p. 012098-12101, 2015.
Chapiro, G., de Souza, A.J., Asymptotic approximation for counterflow combustion in porous media., Applicable Analysis, v. online, p. 1-15, 2015.
Chapiro, G., Furtado, L., Marchesin, D., Schecter, S., Stability of Interacting Traveling Waves in Reaction-Convection-Diffusion Systems. Discrete and Continuous Dynamical Systems, v. suppl., p. 258-266, 2015.
Chapiro, G., Marchesin, D., Schecter, S., Combustion waves and Riemann solutions in light porous foam. Journal of Hyperbolic Differential Equations, v. 11, p. 295-328, 2014.
Chapiro, G., Mailybaev, A. A., De Souza, A. J., Marchesin, D., Bruining, J., Asymptotic approximation of long-time solution for low-temperature filtration combustion. Computational Geosciences, v. 16, p. 799-808, 2012.
Thermal flows in Porous Media
The aim of this project consists in modeling complex physical phenomena in a simple way in order to make analytical techniques possible to be applied. Two interesting problems that are studied following this idea are: (1) Recovery of shale gas by using combustion and (2) Microwave stimulated water flooding.
Related papers
Paz, P., Z., S., Hollmann, T., H., Kermen, E., Chapiro, G., Slob, E., Zitha, P., L., J., EM heating stimulated water flooding for medium-heavy oil recovery. Transport in Porous Media, V. 119, Issue 1, p. 57–75, 2017.
Chapiro, G., Bruining, J., Combustion enhance recovery of shale gas. Journal of Petroleum Science & Engineering, v. 127, p. 179-189, 2015.
Chapiro, G., Bruining, J., Thermal Well Stimulation in Gas Shales Through Oxygen Injection and Combustion. In: Fourth EAGE Shale Workshop, 2014
Population dynamics
The global incidences of Dengue and, more recently, Zica virus have increased the interest in studying and understanding the mosquito population dynamics. This project is based on the study of nonlinear mathematical models dealing with the life cycle of the dengue mosquito using partial differential equations.
Related papers
W. M. S. Yamashita, S. S. Das and, G. Chapiro., Numerical modeling of mosquito population dynamics of Aedes aegypti, Parasites & Vectors, v. 11:245, 2018
Yamashita, W., M., S., Takahashi, L., T., Chapiro, G., Traveling wave solutions for the dispersive models describing population dynamics of Aedes aegypti. Mathematics and Computers in Simulation, , v.146, 90-99, 2018.Yamashita, W., M., S., Takahashi, L., T., Chapiro, G., Dispersive models describing mosquitoes' population dynamics. Journal of Physics. Conference Series (Online), v. 738, p. 012065, 2016.
Inverse problems, Regularization, and Optimization
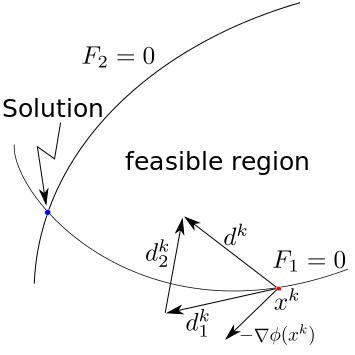
Parabolic-type problems, involving a variational complementarity formulation, arise in mathematical models of several applications in Engineering, Economy, Biology, and different branches of Physics. These kinds of problems present several analytical and numerical difficulties related, for example, to time evolution and a moving boundary. We develop numerical methods that employ a global convergent nonlinear complementarity (or mixed complementarity) algorithms for solving a discretized problem at each time step. Space discretization is implemented using the finite difference implicit scheme and the finite element method.
Some interesting topics involve Regularization techniques and Inverse Problems.
Related papers
Vigo, D. G. A., Cruz, A. A., Chapiro, G., Garcia, G. C., MOREIRA, C. G. T. A., Solving the inverse problem for an ordinary differential equation using conjugation. Journal of Computational Dynamics, v. 7, p. 183-208, 2020.
A. C. Alvarez, Grigori Chapiro, G. C. Garcia, Carlos Gustavo Tamm de A. Moreira. Analysis of regularization by conjugation for bounded linear operators. Preprint. 2017
Gutierrez, A., Mazorche, S., R., Herskovits, J., Chapiro, G. An Interior Point Algorithm for Mixed Complementarity Nonlinear Problems, Journal of Optimization Theory and Applications, online, 1-18, 2017
Chapiro, G., Gutierrez, A., E., R., Herskovits, J., N., Mazorche, S., R., Pereira, W., S., Numerical Solution of a Class of Moving Boundary Problems with a Nonlinear Complementarity Approach. Journal of Optimization Theory and Applications, v. 168, p. 534-550, 2016.
Chapiro, G., Mazorche, S. R., Herskovits, J., Roche, J. R., Solution of the non-linear parabolic problems using nonlinear complementarity algorithm (fda-ncp). Mecánica Computacional, V. XXIX, P. 2141-2153, 2010.
Others
Some collaboration works.
Related papers
Castardelli, R., S., Chapiro, G., Shapiro, I., L., Beyond the linear analysis of stability in higher derivative gravity with the Bianchi-I metric. PHYSICAL REVIEW D, v. 100, p. 066004, 2019.
Chapiro, G., Faria, L.F.O., Maldonado, A.D., On the existence of solutions for a class of fourth order differential equations. Journal of Mathematical Analysis and Applications (Print), v. 427, p. 126-139, 2015.